Introduction

Sorting is a process of arranging a list of items in an order, so that the items in the list are arranged either in ascending order or descending order. Sorting is a very common process that we can also see it in our daily lives, like the contacts application on our phone where we have a list of saved names that are alphabetically sorted in the ascending order (A->Z), or on the e-commerce websites where we can sort the listed items by the prices either in the ascending order (low to high) or the descending order (high to low). These sorting processes are internally performed using different types of sorting algorithms. We will discuss Bubble Sort today!

Bubble Sort is a comparison sort algorithm. We use a logic to swap two adjacent elements in the list to completely sort the list of elements. It is also known as an in-place sorting algorithm, which means that we can sort the items only by modifying the position of the items and not using a new array (using constant space). So, without further ado, let's jump right into the flow to learn Bubble Sort.

Scope

• Bubble Sort (a.k.a. Sinking sort or Exchange sort) Algorithm
• Java Program for Bubble Sort
• Optimized Bubble Sort
• Space and Time complexity analysis

Algorithm for Bubble Sort (Ascending Order)

First, let's see, what are we going to do in the bubble sort algorithm, and then we will jump right onto the how we gonna do it part. So, let's begin!

What are we doing?

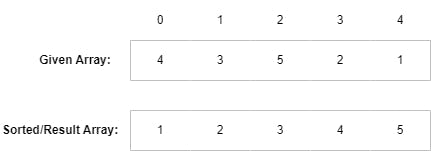
Let's suppose, we have been given an array [4, 3, 5, 2, 1] (sorted array should be [1, 2, 3, 4, 5]). We are going to perform swaps step-by-step (swap simply means to exchange the array elements):

Step 0: We check if the element at index j (starting from j = 0) is greater than the element at index j + 1, we perform the swap and increment the index values, or else we just increment the index values.

Step 0.1: We check the element at index 0 (4) with the element at index 1 (3). Here, arr[0] (4) is greater than arr[1] (3), so we perform the swapping logic and increment the indexes.

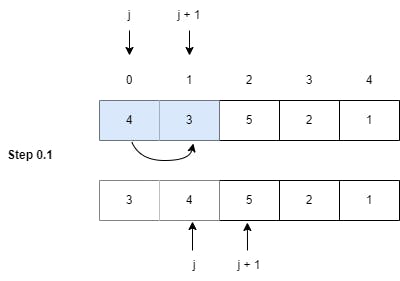
(Swapped the elements as 4 > 3)

Step 0.2: We have incremented the indexes by 1 (j++), now we repeat the same procedure. We check the element at index 1 (4) with the element at index 2 (5). Here, arr[1] (4) is not greater than arr[2] (5). Here, we just increment the indexes.

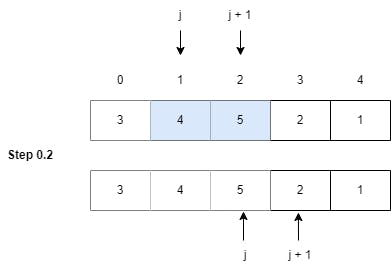
(Here, no swap has been performed as 4 is not greater than 5)

Step 0.3: Now, we check the element at index 2 (5) with the element at index 3 (2). Here, arr[2] (5) is greater than arr[3] (2), so we perform the swapping logic and increment the indexes.

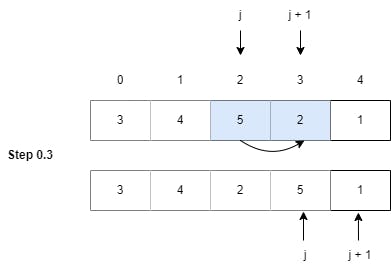
(Swapped the elements as 5 > 2)

Step 0.4: Now, we check the element at index 3 (5) with the element at index 4 (1). Here, arr[3] (5) is greater than arr[4] (1), so we perform the swapping logic and increment the indexes.

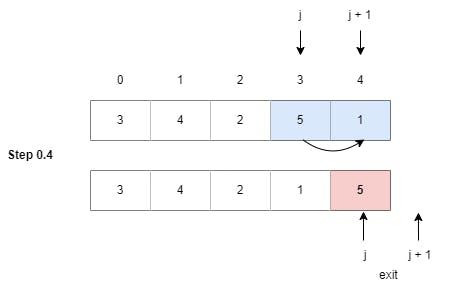
(Swapped the elements as 5 > 1)

Note: As we have completed Step 0, we can see that the largest element in the array has been shifted to the last index of the array, i.e., the last index of the array is now sorted. This also means that we will take our j pointer to check one less element in the next step.

Step 1: We revert the pointer j to point to index 0 and again execute the same approach as Step 0. We check if the element at index j is greater than the element at index j + 1, we swap the elements and increment the index values, or else we just increment the indexes.

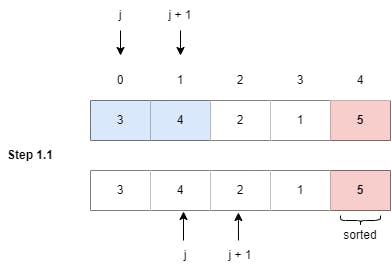
Step 1.1: No swaps performed as 3 is not greater than 4, (j = 0).

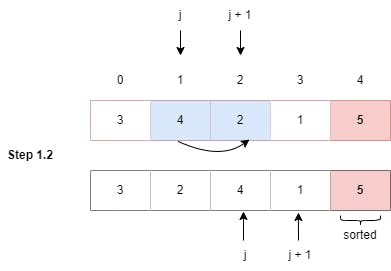
Step 1.2: Swapped elements at index 1 and 2 as (4 > 2), (j = 1).

Step 1.3: Swapped elements at index 2 and 3 as (4 > 1), (j = 2).

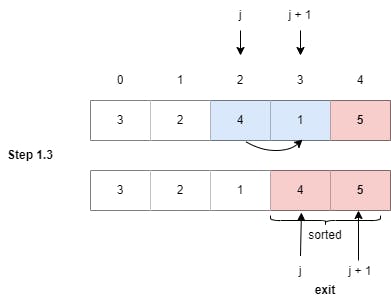
Note: As we have completed the Step 1, we can see that the 2nd largest element in the array has been shifted to the 2nd last index of the array, i.e., the last two indexes of the array are now sorted. This also means that we will take our j pointer to check one more less element in the next step.

Step 2: We revert the pointer j to point to index 0 and again execute the same approach as Step 0.

Step 2.1: Swapped elements at index 0 and 1 as (3 > 2), (j = 0).

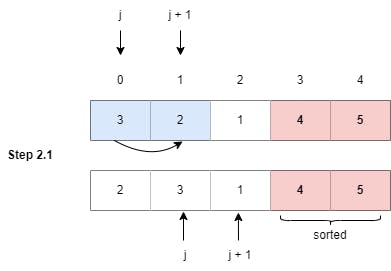
Step 2.2: Swapped elements at index 1 and 2 as (3 > 1), (j = 1).

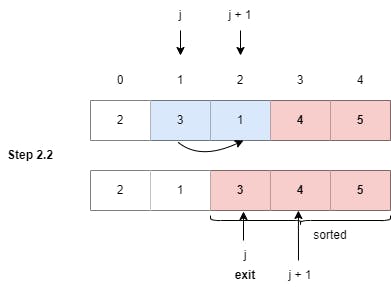
Note: As we have completed the Step 2, we can see that the 3rd largest element in the array has been shifted to the 3rd last index of the array, i.e., the last three indexes of the array are now sorted. This also means that we will take our j pointer to check one more less element in the next step.

Step 3: We revert the pointer j to point to index 0 and again execute the same approach as Step 0.

Step 3.1: Swapped elements at index 0 and 1 as (2 > 1), (j = 0).

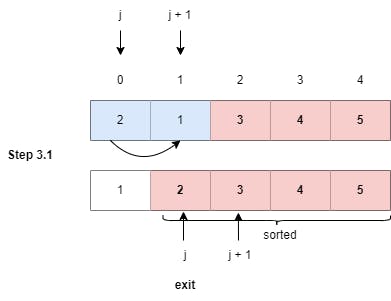
Note: As we have completed the Step 3, we can see that the 4th largest element in the array has been shifted to the 4th last index of the array, i.e., the last four indexes of the array are now sorted!

Step 4: As we have sorted all the elements between the indexes 1 to n-1 (n being the length of the array), the element at index 0 will already be sorted, so we don't have to check whether it is greater than the next element or not. This implies that the whole array has been sorted!

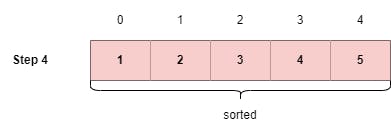
Now, let's see how we can convert the above approach into an algorithm that will help us to program a solution for Bubble Sorting.

How we are doing it? (Flow Algorithm for Bubble Sort)

• First, we have to initialize an array of elements or take user input for the array elements in the main method.
• Then, we call the bubbleSort(arr) method (passing the arr as a parameter in the function), which will shift the control to the bubbleSort() method.
• We run a nested for loop in the bubbleSort() function to traverse the input array.
• Iterator i from the outer for loop will represent our steps count and Iterator j from the inner for loop will be used to compare the adjacent values at each step, such that 0 ≤ i < n-1 and 0 ≤ j < n-i-1, where n is the length of the array.
• Now, we check if arr[j] is greater than arr[j+1], if yes then we swap these adjacent elements, or else we just move on to the next iteration.
• When both the loops terminate, that means our array has been sorted (generally, we don't return the objects (array in this case) in java as the reference to the array is passed to the bubbleSort() function, also due to in-place sorting we are not using a new array).
• Lastly, when the control comes back to the main() function, we print the sorted array using the Arrays.toString() method in Java.

Java Program for Bubble Sort

Optimizing Bubble Sort Algorithm

Now, that we have seen how bubble sort works with java code, we can see how we can optimize it. We can use a flag to check if any swap has taken place on the array or not. If no elements were swapped in the inner loop, the flag remains unchanged, and that means our array is in sorted condition. Now, we don't have to continue the loop, so we can just terminate the outer loop.

Optimized Java Program:

Static Code for Bubble Sort Java (GitHub)

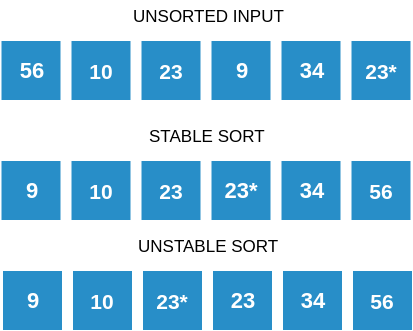
Note: Bubble sort is a stable sorting algorithm as it maintains the order if equal elements are present in the array.

Space and Time Complexity Analysis for Bubble Sort

Recommended to visit Asymptotic Notations and Guidelines for Asymptotic Notations.

Time Complexity for Bubble Sort

Best Case: When the array is sorted, the optimized bubble sort algorithm takes O(n) time.

Worst Case: When the array is sorted in reverse order, the optimized algorithm takes O(n²).

Average Case: As we are running two loops for the length of the array, the average case time complexity also comes out to be O(n²).

Space Complexity for Bubble Sort

Space complexity for the bubble sort algorithm is O(1), as it is an in-place sorting algorithm and doesn't take up any extra space to sort the array.

Outro

Thank you for reading this article, I hope that you were able to understand how bubble sort algorithms work. Try to play around with the code, use different input arrays, and use pen and paper to see how the algorithm works. Afterward, please leave a like and share it with your friends and family!

Happy Coding! :))

Reference: Kunal Kushwaha